Among our crosswords and other puzzles, we’ll be featuring logic challenges from Puzzle Communication Nikoli, a cult-favorite puzzle publication from Japan. A PDF of the puzzle, as well as the solution, can be downloaded below.

Yellow Crow might be called a master of the “pencil puzzle.” As a child, he began with educational logic puzzles and quickly moved on to Sudoku and crosswords. At an elementary school fair he encountered Nurikabe, one of the most popular puzzles from Japan’s Puzzle Communication Nikoli, the most influential puzzle publication in history. Nikoli is famed not just for making Sudoku a household name, but also for being created almost entirely by fans like Yellow Crow.

Many of those readers submit hand-crafted examples of existing puzzles. Yellow Crow, like the creator named Gesaku who created Tentai Show, previously featured on Atlas Obscura, was one of the rare readers who created his own, and he was Nikoli’s youngest. He created the puzzle that came to be known as Pencils when he was in his early teens.

His inspiration came from a simple question: Sudoku and many of Nikoli’s puzzles are called “pencil puzzles”—it’s best to avoid doing these puzzles with a pen—so why not create a new puzzle that actually makes pencils an element? This began a process of trial and error involving straight pencils and turning lines. The result, first introduced in 2017, was unique among Nikoli’s puzzles and was an instant hit with readers.

The solving process, according to Nikoli president, and puzzle creator and editor, Yoshinao Anpuku, is reminiscent of the practice of zen, or a Japanese tea ceremony. Despite the youth of its creator, the puzzle takes something as simple and ordinary as the pencil used to solve it and creates an extraordinary pattern—a representation of the puzzle-solving process itself.

A Pencils puzzle consists of a grid that starts with some combination of numbers and pencil tips. By the end, every cell in the grid must be filled with either a pencil or a line from the tip of a pencil. Each pencil is a straight sequence of cells with a tip at the end. From the tip of each pencil there must be a line—as if drawn by the pencil—passing through a number of cells equal to the size of the pencil itself (minus the tip). While the pencils are straight, the line may turn at right angles as it passes through cells, but it can’t cross or branch off.

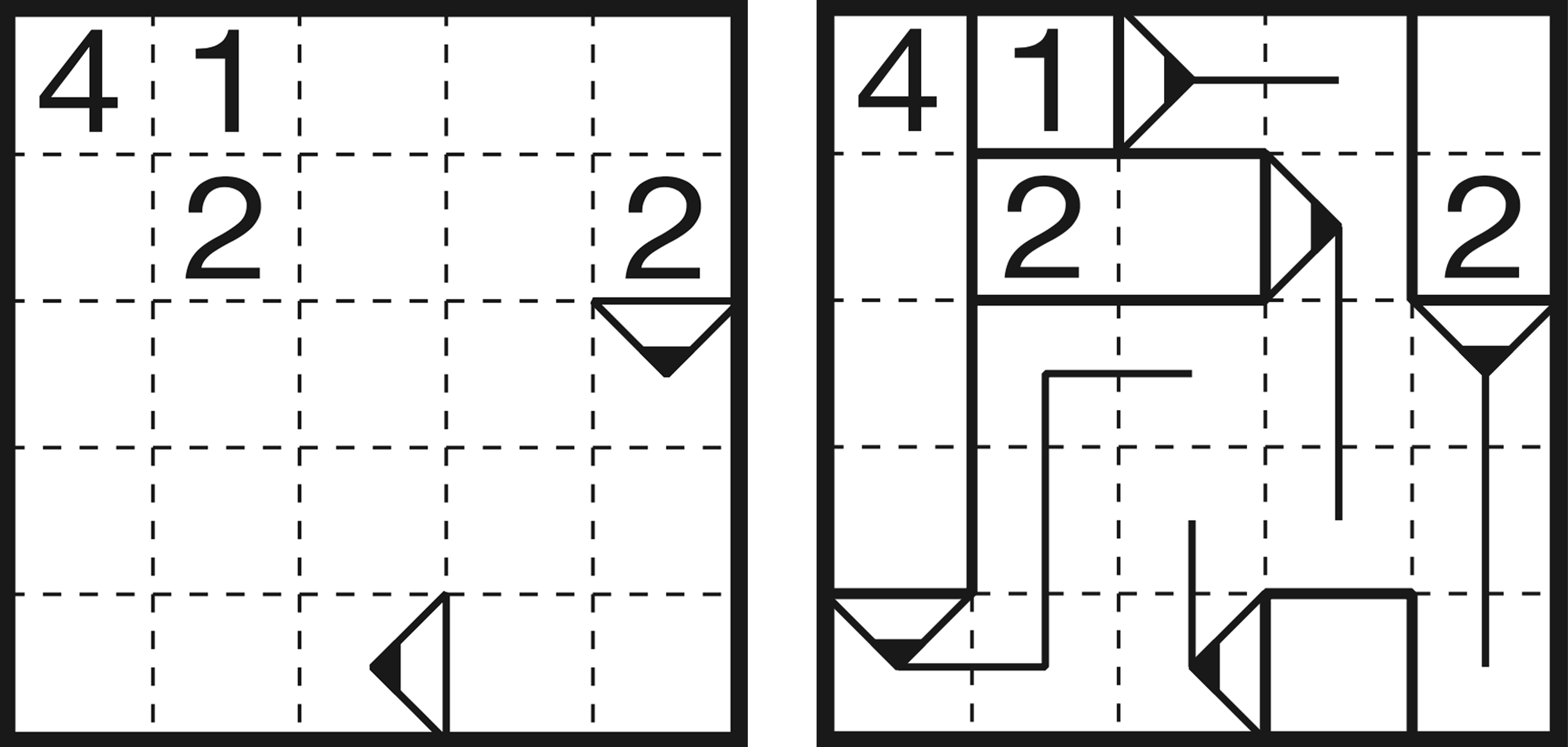
Example puzzle and solution
Example puzzle and solution

For example, a pencil that is four cells long will consist of four consecutive cells (horizontal or vertical) and a cell occupied by the tip. Then a line that extends from that tip through the centers of four additional cells.

The numbers show the length of the pencil that contains that square. A pencil may contain zero, one, or several (of the same) numbers within it. You also may have to draw the tip of a pencil!

In the downloadable PDF below, you’ll find the instructions above, an example, and three puzzles of increasing difficulty.

Stumped? Download the solutions!