Editor’s Note, November 2024: Thanks for checking out our puzzle archive! While the online version of this puzzle is no longer interactive, we suggest downloading the PDF, available below. You can find other archived puzzle PDFs available for download here.

Among our crosswords and other puzzles, we’re featuring logic challenges from Puzzle Communication Nikoli, a cult-favorite puzzle publication from Japan. A PDF of the puzzle, as well as the solution, can be downloaded below.

At 32 years of age, Hashiwokakero is one of the older puzzles in Japan’s Puzzle Communication Nikoli, the most influential puzzle publication in history. It was created by a reader and puzzle constructor—many of puzzle designs are conceived and improved by dedicated readers—using the pen name “Lenin.” He did not choose this name in honor of the Russian revolutionary figure. His real name reads as “Lenin” in Chinese characters.

But this Lenin is also a legend, as he is the mind behind two of the most beloved and widely known Nikoli logic puzzles: Slitherlink and Nurikabe. Hashiwokakero, another one of his enduring creations, can mean a lot of things to a lot of people. For a city dweller, it might look like a transit puzzle, connecting stations in a subway system. For someone on the coast, it looks like building bridges between islands. But neither were Lenin’s inspiration.

Rather, he was inspired by the diagrams that illustrate molecular bonding in chemistry. Anyone who has taken a chemistry class will see the resemblance—single bonds and double bonds creating a solution with the elegance of an amino acid structure. An earlier version of the puzzle he submitted was called Ketsugo-shu (Atomic Bonding). Once he submitted the final, evolved version, he’d switched the metaphor of the title: Hashiwokakero means “Build Bridges.”

Hashiwokakero stands out among other Nikoli puzzles. Though it is grid-based, there is no actual grid present, only circles containing numbers. Your task is to draw connections between the circles. Each island (circle with a number) is connected to the others by one or more bridges. The number denotes how many bridges serve that island.

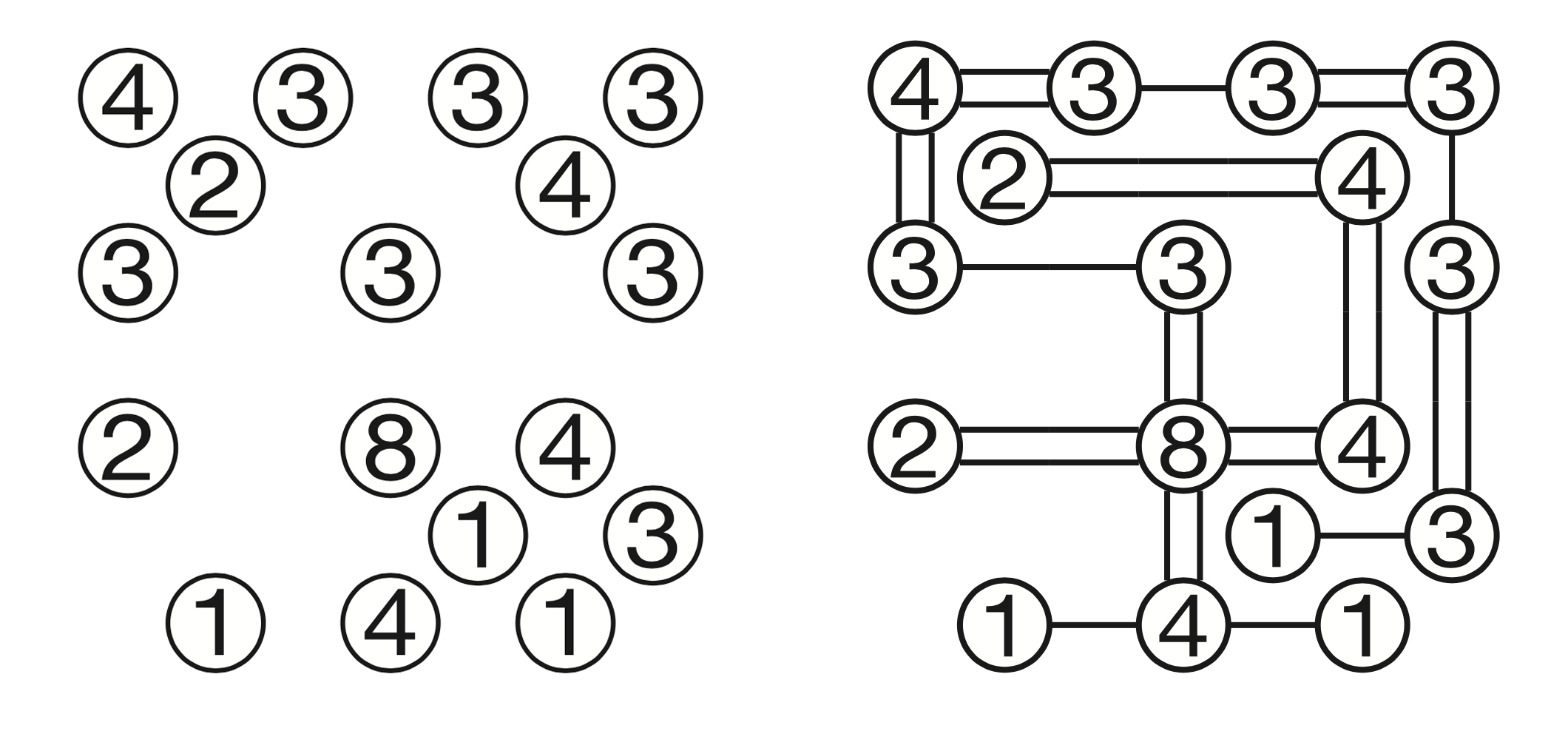
Example puzzle and solution
Example puzzle and solution

Bridges can only go straight up, down, left, or right. There can be no more than two bridges connecting two islands. The bridges may not cross other bridges or islands. Each island must be connected to all the others by a continuous link of bridges.



Stumped? Download the solutions!