Editor’s Note, November 2024: Thanks for checking out our puzzle archive! While the online version of this puzzle is no longer interactive, we suggest downloading the PDF, available below. You can find other archived puzzle PDFs available for download here.

Among our crosswords and other puzzles, we’ll be featuring logic challenges from Puzzle Communication Nikoli, a cult-favorite puzzle publication from Japan. A PDF of the puzzle, as well as the solution, can be downloaded below.

Mazes have existed for thousands of years and might be thought of as the very first puzzles in the world; based on the number of people who’ve likely solved them over the years, they might be the most popular form ever. So it is natural that many puzzle creators, including the readers of Puzzle Communication Nikoli, Japan’s influential, reader-driven puzzle magazine, would try to adapt them to the style of grid puzzle that the publication made famous.

This effort goes back to Maki Kaji, founder of Nikoli, also known as the “Godfather of Sudoku.” He created a a puzzle in which you line up letters in a maze and follow the correct path to form a sentence. This is a puzzle was more about the fun of the resulting sentences than the puzzle or maze itself. Since then, many others tried and failed to make a popular puzzle that combined the Nikoli grid with mazes.

The creator who goes by the pseudonym Bay Wolf finally cracked the code in 2013 with what became Nurimeizu, and he did it by adapting rules from other Nilkoli puzzles. He took the concept of “rooms” from Tilepaint, and the idea of limiting the size of areas from Nurikabe. This is a common practice among new Nikoli puzzles, remixing and reusing rules and mechanics from older, popular puzzle to create a whole new form.

In this case, Bay Wolf finally managed to make a satisfying logic puzzle that creates its own maze at the same time.

And if you love mazes, check out Altas Obscura’s original creations from world record–holding maze maker Michelle Boggess-Nunley:


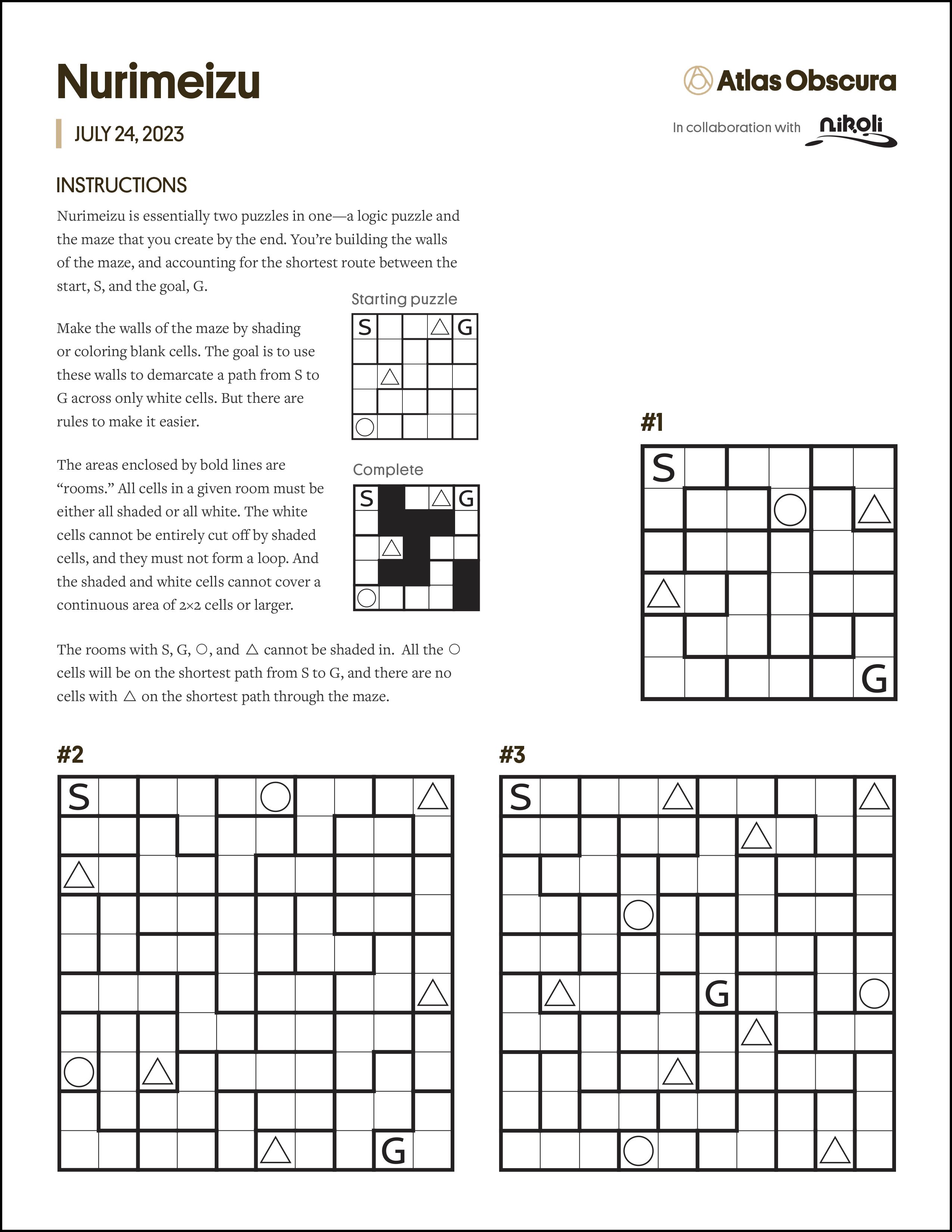
Nurimeizu is essentially two puzzles in one—a logic puzzle and the maze that you create by the end. You’re building the walls of the maze, and accounting for the shortest route between the start, S, and the goal, G.

Make the walls of the maze by shading or coloring blank cells. The goal is to use these walls to demarcate a path from S to G across only white cells. But there are rules to make it easier. The areas enclosed by bold lines are “rooms.” All cells in a given room must be either all shaded or all white. The white cells cannot be entirely cut off by shaded cells, and they must not form a loop. And the shaded and white cells cannot cover a continuous area of 2×2 cells or larger. The rooms with Ｓ, Ｇ, ○, and △ cannot be shaded in. All the ○ cells will be on the shortest path from S to G, and there are no cells with △ on the shortest path through the maze.

Stumped? Download the solutions!