
Puzzle Monday: Breaking the Grid
Editor’s Note, November 2024: Thanks for checking out our puzzle archive! While the online version of this puzzle is no longer interactive, we suggest downloading the PDF, available below. You can find other archived puzzle PDFs available for download here.
Among our crosswords and other puzzles, we’ll be featuring logic challenges from Puzzle Communication Nikoli, a cult-favorite puzzle publication from Japan. A PDF of the puzzle, as well as the solution, can be downloaded below.
One of the most satisfying sights for a lover of pencil or logic puzzles—such as Sudoku and the range of other puzzles from Japan’s Puzzle Communication Nikoli that we’ve featured recently—is a fully completed puzzle. It’s not as clean or orderly as the starting grid, but it’s complete, everything in its place and governed by its own rules.
Among the challenges in Puzzle Communication Nikoli, the world’s most influential puzzle publication, perhaps none are more visually satisfying than Shakashaka, a dance of negative, white space turned 45 degrees from the starting grid. From a simple grid with numbers—one that looks a lot like the starting grid of Akari, which we featured last month, comes a surprising piece of modernist art.

Shakashaka was first introduced in 2008, created, as many Nikoli puzzles are, by a reader. Guten, as the creator is known, has not created many puzzles, but those he has are known for their elegant, complex design. In this case he employs a shape that rarely appears in logic puzzles: the triangle. Many Nikoli puzzles are refinements of earlier puzzles, or lead to other ideas. But that’s not the case with Shakashaka—it has no precedent or antecedent.
According to Nikoli president and puzzle editor Yoshinao Anpuku, a completed Shakashaka puzzle might at first appear a little “grotesque,” seeming to defy the normal, grid-based logic of many of Nikoli’s favorites. “But for some reason, many people thought it was a ‘soothing pattern,’” he says, offering “a sense of security.”
It wasn’t just the visual appeal of a completed puzzle that drove Shakashaka to become a hit; it’s also fun, with a lot of different possible solving techniques.
The goal of the puzzle is to place black triangles in the grid’s white cells according to the following rules:
- A black triangle—connecting opposite corners of a square cell—can be drawn and filled in any of four different ways.

- Any white cell can host a triangle, but they don’t all need to be filled in.
- The numbered cells indicate how many triangles appear adjacent to that cell.
- The grid must be filled in such a way that each patch of remaining white space forms a rectangle or square. These rectangles might be oriented in the same direction as the grid, or at a 45-degree angle.
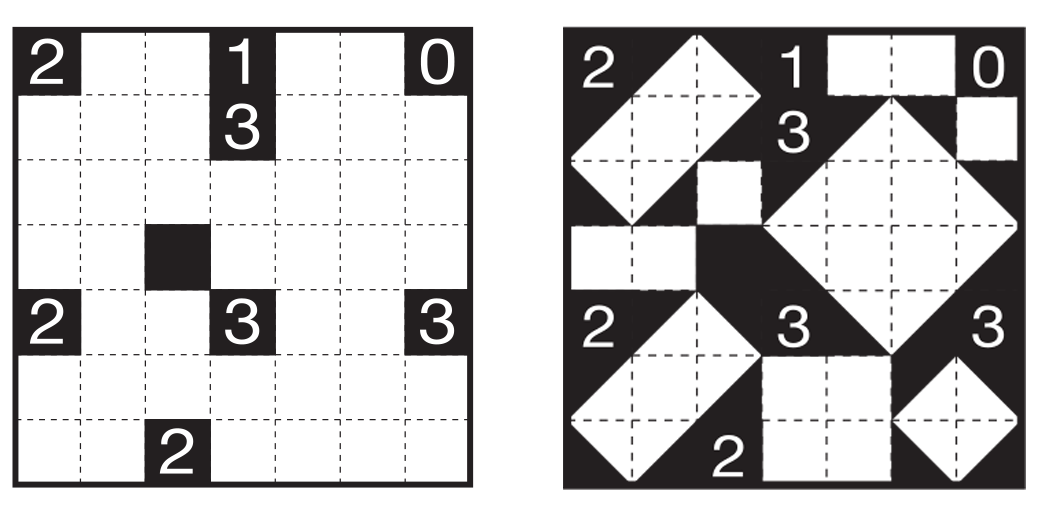
You should begin by placing triangles around numbered cells where you can, especially in corners and along edges. Remember the number one rule of Shakashaka: Never create an acute angle!

Stumped? Download the solutions!









Follow us on Twitter to get the latest on the world's hidden wonders.
Like us on Facebook to get the latest on the world's hidden wonders.
Follow us on Twitter Like us on Facebook