The Satisfaction of Mathematically Efficient Christmas Cookies
If only there were a cookie-cutter solution.
This December, Martin Lersch, a Norwegian chemist and a passionate cook, rolled out his homemade gingerbread dough and got to work. He flipped his cookie cutter to and fro repeatedly, creating a quilt of cookies in the shape of Christmas trees. But Lersch’s main goal wasn’t simply a batch of delicious holiday cookies. He wanted to bake mathematically perfect ones.
For the last few years, Lersch has attempted to solve a problem that often bedevils cookie bakers. “You want to make best possible use of the dough without having to collect all the in-betweens and knead it together and roll out again,” says Lersch. “It’s really about saving time.”
Lersch took up Christmas cookie baking as a project for his blog, Khymos, where he explores the chemistry and science of cooking. Common holiday cookie shapes, he’s found, don’t typically fit together very neatly. Bulbous Santas, candy canes, and gingerbread men tend to leave lots of dough scraps behind. In his quest for a festive yet efficient cookie cutter, he’s designed a shape that can punch out neat ranks of cookies with minimal leftover dough. Lersch’s Christmas tree, as it happens, can be tessellated.
Popularized by the Dutch printmaker and artist M.C. Escher and a longtime feature of Islamic art, tessellations are geometric shapes that fit together perfectly. (Think mosaics, puzzles, or Tetris when you’re playing to win.) Many of these tessellations repeat over and over again, like a wallpaper pattern, and all are dizzying when viewed at scale.
Lersch set out to design a cookie cutter that could turn a rolled-out sheet of dough into a tessellated plane, meaning no left-over space between each shape. Escher once wrote that he found the complexity of the trippy patterns “great fun,” because of their ability “to confuse two and three dimensions.” And it’s true that tessellations have long confused both math’s greatest minds and its most advanced algorithms.

Cutting cookies may not feel like you’re working out an equation on gingerbread, but that’s what’s at work mathematically, according to a recent study. Mikkel Abrahamsen, a mathematician at the University of Copenhagen and the lead author of the paper, researches the packing problem. The packing problem is something that businesses and designers face every day, as they calculate how to fit as many objects as possible in a limited space. As you can imagine, the packing problem has implications on everything from the shipping industry to storing spices in your kitchen pantry.
Abrahamsen specializes in how algorithms can be expressed in geometric terms—precisely what’s happening when you press a cookie cutter into a 2-D, doughy canvas. “What we wanted to do is to prove that when you solve these packing problems, then you are actually forced to solve very complicated equations,” he says.
The packing problem is a ∃R-complete equation, Abrahamsen’s team argues, a step in complexity beyond the non-polynomial equations that have long been studied by computer scientists. The problem’s complexity lies in part with the number of variables involved. In order to solve for the optimal packing—a tessellation which would use as much of a sheet of rolled-out dough as possible—Abrahamsen says one would need to know the ideal placement of every single cookie in advance. The problem is, there are endless ways to orient cookie shapes on a sheet of dough. Plus, with every stamp of the cookie cutter, the amount of space you’d have for more cookies gets smaller. Without a computer program to help you out, you’d likely only realize the effectiveness of your packing as you ran out of space. “You would need to try an infinite number of possibilities before you find the best [solution],” Abrahamsen says.

This didn’t stop Lersch, though, who created his own Christmas-themed tessellations of bells, Christmas trees, and other shapes using the free-to-use platform Tess. With help from a friend, he 3D-printed several cookie cutters and mixed up some dough. Lersch’s cookie of choice, pepperkake, is a sumptuous Norwegian gingerbread. Lersch, primarily a chemist, notes that it was once made with ammonium carbonate from ground deer antlers, though most people substitute baking powder these days.
After deciding on the Christmas tree as the most efficient shape, Lersch then got to work. Emulating Escher’s patterns, he stamped every other tree shape right-side-up, to fit perfectly with the trees around it, which he stamped upside-down. The result? Interlocking rows of cookies, with no leftover dough left between their lines.
But even with Lersch’s cookie cutter, scraps of dough will linger at the edges of the pattern. This is the imperfection that Abrahamsen warned about: there are simply too many variables to make a cookie cutter in a complex shape that uses a whole slab of rolled-out dough, all at once, every time. To maximize efficiency, you could make your cookies a simpler shape: for example, square cookies, cut from a square piece of dough. But, as Lersch says, “Who wants square cookies?”

With complex shapes such as Christmas trees, Abrahamsen says finding the single most efficient way to arrange them on a pane of dough is, as of today, impossible. In 1999, an algorithm was only able to solve the packing problem in a square container for up to four objects—simple heptagons—and it took the program 24 hours to get the job done. It became harder for the algorithm to solve the problem with each new polygon thrown into the equation, just as it becomes harder to pack anything into a container when space is already occupied. To Abrahamsen’s knowledge, no faster algorithm has been found since.
But baking isn’t always about the pursuit of perfection. Simply trying to create the most effective method of slicing up some festive cookies should be encouraged, says Abrahamsen. “I would advise [people] to do it … for the joy of the puzzle,” he says. “It’s good to think about it, but they shouldn’t expect to find the optimal solution.”
Lersch agrees that there may be no way to make a mathematically perfect batch of holiday cookies at the moment. The world might need to wait for an even more suitable shape than his tree (which, a few years ago, Lersch’s friend put online for anyone to download. Merry Christmas!) But he still encourages baking in tessellations, if only for personal enjoyment and “nerding out,” he says. “If this can reduce the fear that some people have of mathematics or science,” he adds, “even better.”
Gastro Obscura covers the world’s most wondrous food and drink.
Sign up for our email, delivered twice a week.









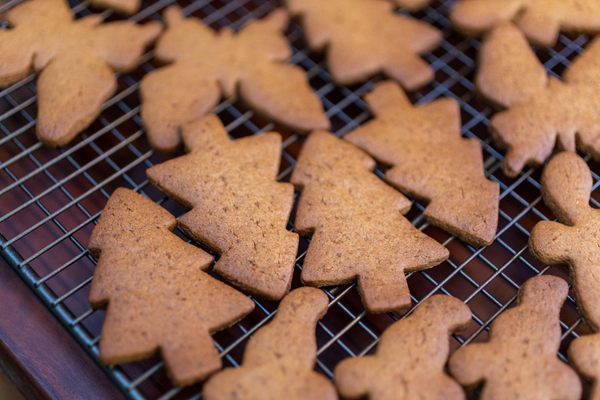















Follow us on Twitter to get the latest on the world's hidden wonders.
Like us on Facebook to get the latest on the world's hidden wonders.
Follow us on Twitter Like us on Facebook